The finite element, parallel PN-transport solver based on domain-decomposition PARAFISH
The increasing computer power nowadays available in HPC pave the way for the development of full parallel codes that solve the Boltzmann transport equation with less approximation using transport methods instead of diffusion methods and domain decomposition to take profit of the HPC-architecture. Hence, the PARAFISH code is being developed and validated at KIT for high-fidelity simulations of reactor cores as it can be done with Monte Carlo solvers.
PARAFISH (PARAllel Finite-element Spherical Harmonic) code is a 3D parallel neutron transport code written in C++ being developed at the Karlsruhe Institute for Technology to solve the static Boltzmann Transport Equation (BTE) in order to describe the core neutronics. At present, two kind of simulations can be done: fixed-source and criticality calculations. PARAFISH solves the so-called even parity formulation of the BTE, where only the even part of the angular dependence is computed. The spatial discretization is based on finite elements for the spatial dependence, and spherical harmonic expansions for the angular dependence. In addition, an algebraic non-overlapping domain-decomposition method is introduced along the lines of modified Schwarz methods.
PARAFISH Perspectives
The code is under development and validation phase for static simulations. Further improvements will be focused on:
- Optimization of the domain decomposition method and parallel scalability
- Implementation of cross section generation format for handling of cross section for core analysis
- Implementation of a ICoCo-method for coupling with TH-solver such as TwoPorFlow or SubChanFlow
- Implementation of a time dependent solution
- Application to industry-like applications
PARAFISH Current applications
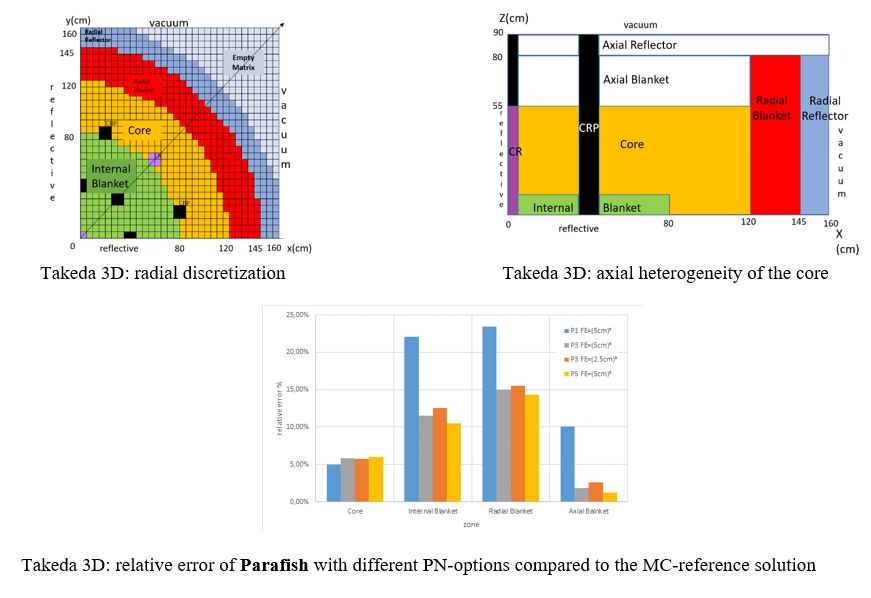
Analysis of the TAKEDA 3D problem with axial heterogeinity
Papers
- S. Van Criekingen. PARAFISH: A Parallel FE−PN Neutron Transport Solver based on Domain Decomposition (also in Parafish/Parafish_Code/parafish/branches/export/DocExtra)
- S. Van Criekingen, F. Nataf, P. Havé. PARAFISH: A parallel FE–PN neutron transport solver based on domain decomposition, Annals of Nuclear Energy 38 (2011) 145-150
- S. Van Criekingen. Domain Decomposition PN Solutions to the 3D Transport Benchmark over a Range in Parameter Space, 2012
- S. Van Criekingen. A non-conforming generalization of Raviart–Thomas elements to the spherical harmonic form of the even-parity neutron transport equation, Annals of Nuclear Enegy 33 (2006) 573-582
- S. Van Criekingen. A 2-D/3-D Cartesian geometry non-conforming spherical harmonic neutron transport solver, Annals of Nuclear Enegy 34 (2007) 177-187
- C. Subramanian, S. Van Criekingen, V. Heuveline, F. Nataf, P. Havé. The Davidson method as an alternative to power iterations for criticality calculations, Annals of Nuclear Enegy 38 (2011) 2818-2823